| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 프로그래머스
- 다이나믹프로그래밍
- 소수판정
- 자료구조
- C언어
- C
- 구현
- 프로그래머스sql
- 프로그래머스코딩테스트
- 이분탐색
- 백준알고리즘
- 그리디알고리즘
- 문자열
- 정렬
- 백준
- 수학
- MySQL
- 사칙연산
- 해시를사용한집합과맵
- 그리디
- 정수론
- Image Classification
- 논문리뷰
- 이진탐색
- 프로그래머스연습문제
- 논문구현
- 브루트포스알고리즘
- 큐
- C++
- SQL
- Today
- Total
초보 개발자의 이야기, 릿허브
[C++] 백준 1654번 랜선 자르기 본문
1. 문제이해
https://www.acmicpc.net/problem/1654
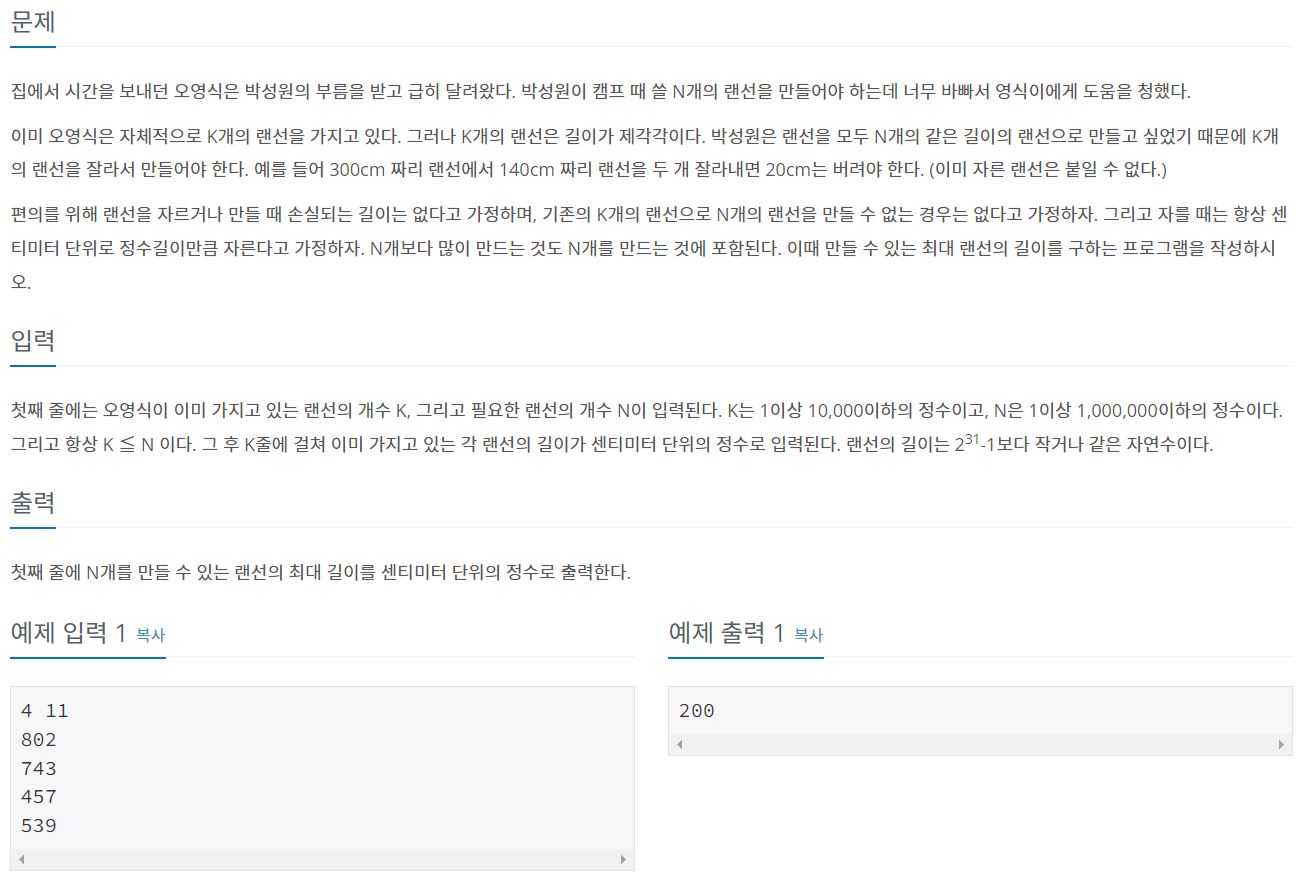
1654번: 랜선 자르기
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그
www.acmicpc.net
오영식이 가지고 있는 랜선의 개수 K와 필요한 랜선의 개수 N이 주어진다.
K개의 랜선을 이용해 N개의 랜선을 얻으려고 할 때, 만들 수 있는 랜선의 최대 길이를 출력하는 것이 목표이다.
단, N개 이상의 랜선을 만드는 것 또한 N개의 랜선을 만드는 것에 포함된다.
2. 문제풀이
K개의 랜선을 가지고 N개 이상의 랜선을 만드려고 할 때, 만들 수 있는 랜선의 최대 길이를 구하는 문제이다.
for문을 통해 무작정 길이를 늘려나가는 방법도 있겠지만,
K와 N의 범위가 크기 때문에 (K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수),
시간초과 방지를 위해 이분탐색을 이용해야한다.
필자는 파라메트릭 서치(Parametric Search) 를 이용했다.
파라메트릭 서치(Parametric Search) 란, 다른 말로 매개변수 탐색이라고도 하며,
최적화 문제를 결정 문제로 바꾸어 푸는 것이다.
여기서 결정 문제란, "예" 또는 "아니오"로 답하는 문제이다.
무슨 이야기냐 하면, 아래 예제를 통해 간단하게 살펴보도록 하자.
몸무게가 70kg 이상인 사람들 중 가장 몸무게가 적은 사람을 찾는다고 하자.
해당 문제를 결정 문제로 바꾸면 다음과 같다.
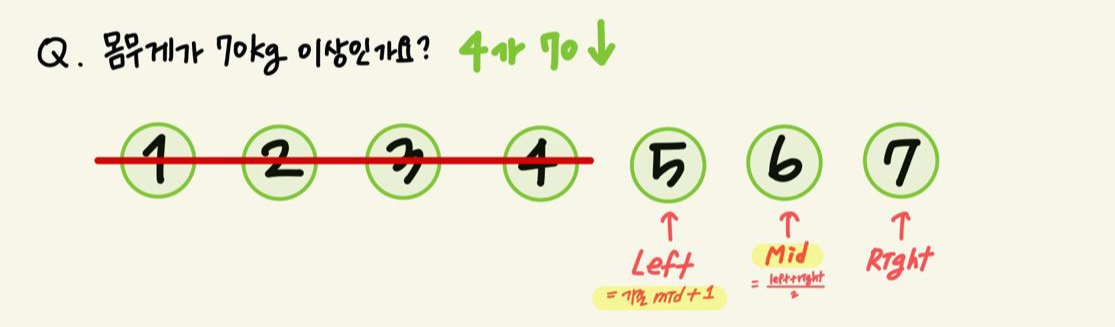
몸무게가 70kg 이상인가요?
이제 주어진 사람들 중에서 조건을 만족하는 사람을 찾아보자.

1. 다음과 같이 7명의 사람들이 있다. (모든 사람들은 몸무게 순으로 정렬되어있다.)
Left와 Right를 다음과 같이 설정한 후, Mid = (Left + Right) / 2 라고 둔다.
이제 Mid부터 결정 문제에 대해 답한다.
Mid = 4 번째 사람은 70kg 이상인가요?
2. Mid = 4 번째 사람은 70kg 이상인가요? 에 대한 답이 "아니오"인 경우이다.
4번째 사람이 70kg 이하이고, 사람들은 몸무게 순서대로 정렬되어있으므로,
4번째 이전의 사람들은 모두 70kg 이하가 된다.
따라서, 5번째 사람부터 다시 Left, Right를 설정해주고 과정을 반복해주어야 한다.
즉, Mid < 조건 인 경우, Left = Mid + 1 로 바꾸어 주어야 한다.
Left 값을 위와 같이 재설정 해준 뒤, 다시 결정 문제에 대해 답한다.
Mid = 6 번째 사람은 70kg 이상인가요?

3. Mid = 6 번째 사람은 70kg 이상인가요? 에 대한 답이 "예"인 경우이다.
6번째 사람이 70kg 이상이므로, 7번째 사람은 70kg 이상이 된다.
그렇다면, 6번째 사람이 바로 70kg 이상인 사람 중 가장 가벼운 사람인가?
아니다. 아직 5번째 사람이 해당 조건을 만족하는지 확인을 하지 못했으므로, 확인이 필요하다.
따라서, 다시 Left, Right를 설정해주고 과정을 반복해주어야 한다.
즉, Mid > 조건 인 경우, Right = Mid - 1 로 바꾸어 주어야 한다.
Right 값을 위와 같이 재설정 해준 뒤, 다시 결정 문제에 대해 답한다.
Mid = 5 번째 사람은 70kg 이상인가요?
4. Mid = 5 번째 사람은 70kg 이상인가요? 에 대한 답이
"예" 라면, 5번째 사람이 조건을 만족하는 사람이 되고,
"아니오" 라면, 6번째 사람이 조건을 만족하는 사람이 된다.
위와 같은 과정을 통해 조건을 만족하는 수를 찾아내는 것이 바로 파라메트릭 서치이다.
보시다시피 이분탐색과 매우 유사하며, 결정조건을 이용해 이분탐색으로 풀이하는것이 파라메트릭 서치이다.
이러한 파라메트릭 서치를 이용해 풀이한 코드는 아래와 같다.
3. 소스코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector <long long> lan;
long long K, N;
long long element;
long long minlan, maxlan, midlan, reslan;
long long cnt;
// num만큼 잘랐을 때 얻을 수 있는 랜선의 수
long long count_lan(long long num) {
cnt = 0;
for (int i = 0; i < K; i++) {
cnt += lan[i] / num;
}
return cnt;
}
// 파라메트릭 서치(Parametric Search)
void parametric_search() {
while (minlan <= maxlan) {
// 1. 중간 지점 설정
midlan = (minlan + maxlan) / 2;
// 2 - 1. mid 만큼 잘랐을 때 만들 수 있는
// 랜선의 개수가 N 개 이상일 경우
// -> 조건은 만족하지만, 최대 랜선의 길이를 구하는 것이므로
// 더 큰값이 있나 확인 필요. min = mid 값 + 1 해서 재탐색
if (count_lan(midlan) >= N) {
reslan = midlan;
minlan = midlan + 1;
}
// 2 - 2. mid 만큼 잘랐을 때 만들 수 있는
// 랜선의 개수가 N 개 이하일 경우
// -> 조건 불만족. 더 작은 범위에서 랜선의 길이를 찾아야함.
// max = mid 값 - 1 해서 재탐색
else {
maxlan = midlan - 1;
}
}
}
int main() {
cin >> K >> N;
for (long long i = 0; i < K; i++) {
cin >> element;
lan.push_back(element);
}
// 탐색에 앞서 정렬
sort(lan.begin(), lan.end());
minlan = 1;
maxlan = lan[K - 1];
parametric_search();
cout << reslan;
return 0;
}N과 K의 범위가 크기때문에, 해당 변수들을 비롯한 모든 변수들을 long long 형으로 선언해준다.
각각의 변수들이 뜻하는 바는 다음과 같다.
vector <long long> lan;
➡ 영식이가 가지고 있는 랜선의 길이
long long K, N;
➡ 각각 영식이가 가진 랜선의 개수, 얻고자 하는 랜선의 개수
long long element;
➡ 랜선의 길이를 입력받기 위한 변수 (cin 통해 벡터값 저장)
long long minlan, maxlan, midlan, reslan;
➡ 파라메트릭 서치를 위한 변수들.(왼쪽값, 오른쪽값, 중간값, 구하고자 하는 값)
long long cnt;
➡ 자르고자 하는 랜선의 길이를 num으로 설정 후 잘랐을 때 얻을 수 있는 랜선의 개수
count_lan 함수는 자르고자하는 랜선의 길이 num을 매개변수로 받아,
num 길이만큼 잘랐을 때 얻을 수 있는 랜선의 개수를 구하는 함수이다.
parametric_search 함수는 이름 그대로 파라메트릭 서치를 수행하는 함수로,
2. 문제풀이에서 구한 방식에 따라 조건을 만족하는 값을 구하는 함수이다.
해당 문제에서의 결정조건은,
중간값만큼 잘랐을 때 얻을 수 있는 랜선의 개수(count_lan(midlan))가 얻고자 하는 랜선의 개수(N)보다 많은가?
즉, count_lan(midlan) >= N ? 이다.
여기서는 위 조건을 만족하는 것들 중 최대값을 구하는 것이기때문에,
해당 조건을 만족하면 minlan = midlan + 1;
만족하지 못하면 maxlan = midlan - 1;
해주고 해당 작업을 반복한다.
메인함수에서는 K, N, 랜선의 길이들을 입력받은 뒤, 탐색을 위해 입력받은 랜선값들을 정렬한다.
min, max 값을 초기화 한 후, parametric_search 함수를 호출해 위 작업을 진행한다.
주석없는 코드는 왼쪽 아래 더보기를 참고바랍니다.😊
<주석 없는 코드>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector <long long> lan;
long long K, N;
long long element;
long long minlan, maxlan, midlan, reslan;
long long cnt;
long long count_lan(long long num) {
cnt = 0;
for (int i = 0; i < K; i++) {
cnt += lan[i] / num;
}
return cnt;
}
void parametric_search() {
while (minlan <= maxlan) {
midlan = (minlan + maxlan) / 2;
if (count_lan(midlan) >= N) {
reslan = midlan;
minlan = midlan + 1;
}
else {
maxlan = midlan - 1;
}
}
}
int main() {
cin >> K >> N;
for (long long i = 0; i < K; i++) {
cin >> element;
lan.push_back(element);
}
sort(lan.begin(), lan.end());
minlan = 1;
maxlan = lan[K - 1];
parametric_search();
cout << reslan;
return 0;
}
이분 탐색 관련 문제들은 너무 약해서..😥
이분탐색과 거의 동일한 파라메트릭 함수 문제를 풀어보았는데, 역시나 어려웠다.
관련 이론은 따로 포스팅해서 정리해놓아도 좋을 것 같다.
'코딩테스트 > 📗 백준 (BOJ)' 카테고리의 다른 글
| [C++] 백준 11931번 수 정렬하기 4 (0) | 2022.02.25 |
|---|---|
| [C++] 백준 10867번 중복 빼고 정렬하기 (0) | 2022.02.24 |
| [C++] 백준 11728번 배열 합치기 (0) | 2022.02.22 |
| [C++] 백준1292번 쉽게 푸는 문제 (0) | 2022.02.18 |
| [C++] 백준 11866번 요세푸스 문제 0 (0) | 2022.02.17 |




