| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 구현
- 자료구조
- 문자열
- 프로그래머스
- 이분탐색
- 논문구현
- 그리디
- C++
- 브루트포스알고리즘
- 백준
- MySQL
- 다이나믹프로그래밍
- 수학
- 그리디알고리즘
- 큐
- 프로그래머스연습문제
- 프로그래머스sql
- 백준알고리즘
- C언어
- 정렬
- 정수론
- 이진탐색
- SQL
- C
- Image Classification
- 논문리뷰
- 소수판정
- 프로그래머스코딩테스트
- 사칙연산
- 해시를사용한집합과맵
- Today
- Total
초보 개발자의 이야기, 릿허브
[C] 백준 1920번 수 찾기 본문
1. 문제이해
https://www.acmicpc.net/problem/1920
1920번: 수 찾기
첫째 줄에 자연수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1 ≤ M ≤ 100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들
www.acmicpc.net
N개의 숫자과 M개의 숫자를 입력받아, M개의 숫자 중에서 N개의 숫자 중
똑같은 값이 있으면 1, 없으면 0을 출력하는 알고리즘을 구현하는 것이 목표이다.
2. 문제풀이
문제 자체는 간단하다.
N, M개의 숫자로 이루어진 수열을 입력받아,
수열 M의 숫자가 수열 N에 있으면 1, 아니면 0을 출력하면 된다.
처음 문제를 보았을 때, 생각보다 문제가 쉽네?
하면서 이중 for문으로 야심차게 구현했으나.. 백준에서는 시간초과가 발생했다.
블로그 포스팅을 하면서 다른 분들의 방법도 찾아보니,
시간초과가 발생하신 분들을 꽤나 많이 찾아볼 수 있었다.
아마 이 포스팅을 보고 있는 분들도 시간초과로 인해 보고 계시지 않을까라는 생각이 든다.
시간을 줄이기 위한 방법으로, 총 2가지 방법을 사용했다.
첫 번째는 이진탐색(이분탐색), 두 번째는 이진탐색을 위한 퀵 소트이다.
첫 번째로 이분탐색 알고리즘은 정렬되어 있는 배열에서 특정한 값을 찾아내는 알고리즘이다.
이는 특정 값을 배열의 중간에 있는 값과 비교하여,
중간값보다 작으면 좌측으로, 크면 우측으로 다시 탐색하는 방식이다.
다음은 이진 탐색을 이용해 77을 찾는 그림이다.
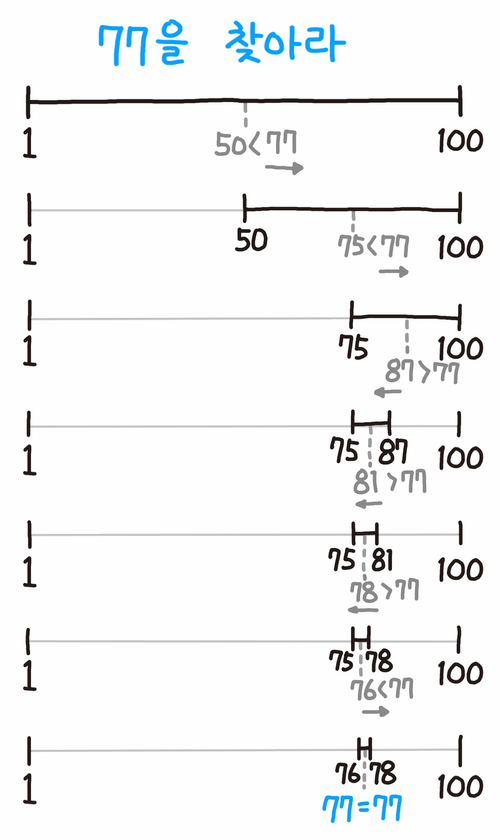
중간값인 50부터 탐색을 시작해, 77이 50보다 크므로 우측을 다시 탐색한다.
다시 50과 100의 중간값인 75를 정하고, 77이 75보다 작으므로 좌측을 탐색한다.
이런식으로 탐색을 계속하다보면, 해당하는 숫자를 맞출 수 있게 된다.
그렇다면, 왜 이중 for문이 아닌 이진탐색(이분탐색)을 사용해야하는 걸까?
결론부터 이야기하자면, 이진 탐색의 시간복잡도는 O(log_2 n), 이중 for문의 시간복잡도는
이진 탐색과 시간 복잡도 분석 (Binary Search and its Time Complexity Analysis) (tistory.com)
이진 탐색과 시간 복잡도 분석 (Binary Search and its Time Complexity Analysis)
오늘 다뤄 볼 주제는 바로 "이진 탐색(Binary Search)" 입니다. 높은 효율을 자랑하며 실제로 자주 쓰이는 알고리즘인데요, 과연 이진 탐색이라는 게 무엇인지 한번 알아봅시다! - 이진 탐색(Binary Searc
jwoop.tistory.com
시간초과를 방지하기 위한 두 번째 방법으로는 이진 탐색 알고리즘에 사용할 퀵 소트이다.
앞서 이야기했듯, 이진 탐색은 정렬된 배열에서 활용하는 알고리즘이다.
따라서, 배열을 한번 정렬을 해줄 필요가 있는데, 이때 사용한 것이 바로 퀵 소트이다.
퀵 소트는 하나의 큰 문제를 두 개의 작은 문제로 나누어 정렬하는 분할과 정복 방식의 정렬로,
쉽게 말해, 특정한 값을 기준으로 큰 숫자와 작은 숫자를 서로 교환하고, 배열을 나누는 방식이다.
퀵 소트는 평균적으로 시간복잡도가 O(nlogn)이며, C의 stdlib.h의 내장함수이므로 간단히 사용할 수 있어,
퀵 소트를 선택하여 이진 탐색을 하기 전, 배열 안의 값을 정렬해주었다.
퀵 소트와 시간복잡도에 대한 더 자세한 설명은 다음 포스팅을 참고하자.
5. 퀵 정렬(Quick Sort) : 네이버 블로그 (naver.com)
5. 퀵 정렬(Quick Sort)
지난 시간까지 다루었던 선택 정렬, 버블 정렬, 삽입 정렬 알고리즘은 모두 시간 복잡도 O(N^2)을 가지는...
blog.naver.com
정렬 알고리즘 - Quick Sort (평균- nlogn, 최악- n^2) (tistory.com)
정렬 알고리즘 - Quick Sort (평균- nlogn, 최악- n^2)
안녕하세요 정렬 알고리즘1 글을 써놓고 2는 바빠서 못썼네요ㅎㅎ.. 오늘은 퀵정렬만 정리해보려고 합니다. 퀵정렬은 개념을 아예 모르시는 분들이 보면 이해하기가 처음엔 힘들어요. 그래서
zeddios.tistory.com
3. 소스코드
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
int arrN[100000];
int arrM[100000];
int check[100000];
// 이진탐색트리
int binary_search_tree(int arr[], int key, int size) {
int front, rear, pivot;
front = 0;
rear = size - 1;
while (1) {
pivot = (front + rear) / 2;
if (arr[pivot] == key) return 1;
if (arr[front] == key) return 1;
if (arr[rear] == key) return 1;
if (arr[pivot] < key)
front = pivot + 1;
else
rear = pivot - 1;
if (front >= rear)
return 0;
}
}
// 퀵 소트에서 사용할 비교함수
int cmp(const void* a, const void* b) {
return *(int*)a > * (int*)b ? 1 : (*(int*)a < *(int*)b ? -1 : 0);
}
int main() {
int N, M;
int i;
scanf("%d", &N);
for (i = 0; i < N; i++) {
scanf("%d", &arrN[i]);
}
scanf("%d", &M);
for (i = 0; i < M; i++) {
scanf("%d", &arrM[i]);
}
// 퀵 소팅
qsort(arrN, N, sizeof(int), cmp);
for (i = 0; i < M; i++) {
printf("%d\n", binary_search_tree(arrN, arrM[i], N));
}
return 0;
}위와 같이, 이진탐색트리와 퀵소트를 이용해 보다 시간을 줄인 알고리즘을 구현하였다.
이진 탐색 트리에서는 기준이 되는 가장 앞의 값(front), 뒤의 값(rear)를 두고,
이의 중간값인 pivot을 계속 변화시켜가며 원하는 값(key)을 찾았다.
퀵 소트를 이용하여 입력받은 N의 배열을 정렬한 후, (main 함수에 구현)
만약 key값을 찾으면 1 을 반환하고, 그렇지 않으면 왼쪽, 오른쪽으로 pivot을 계속 이동 후,
마지막까지 없다면 0을 반환하도록 하였다.
아래 코드는 위애서 언급한 이중 for문을 이용해 구현한 코드이다.
백준에서는 시간초과가 나는 비교적 비효율적인 코드이지만,
이러한 구현방법도 있다는 것을 한번 인지하고 넘어가도 좋을 것 같다.
(자세한 보기는 왼쪽 아래 더보기를 참고하자.)
< 이중 for문을 이용한 소스코드 > (시간초과)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int arrN[100000];
int arrM[100000];
int check[100000];
int main() {
int N, M;
int i, j;
scanf("%d", &N);
for (i = 0; i < N; i++) {
scanf("%d", &arrN[i]);
}
scanf("%d", &M);
for (j = 0; j < M; j++) {
scanf("%d", &arrM[j]);
}
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
if (arrM[i] == arrN[j]) {
check[i] = 1;
break;
}
else
check[i] = 0;
}
}
for (i = 0; i < M; i++) {
printf("%d\n", check[i]);
}
return 0;
}
이중 for문을 쓰고 쉽다고 생각했다가 큰 코 다친 문제였다.
이중 for문을 쓰는 문제였다면 브론즈 정도의 문제였을 것 같다.🤔
나름 배운것이 정말 많은 문제였던 것 같다. 🙂
'코딩테스트 > 📗 백준 (BOJ)' 카테고리의 다른 글
| [C] 백준 1065번 한수 (0) | 2021.08.06 |
|---|---|
| [C++] 백준 1026번 보물 (0) | 2021.08.05 |
| [C] 백준 1978번 소수 찾기 (0) | 2021.08.03 |
| [C] 백준 1002번 터렛 (0) | 2021.08.03 |
| [C++] 백준 1417번 국회의원 선거 (0) | 2021.08.02 |




