| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 프로그래머스코딩테스트
- 이분탐색
- 구현
- C++
- C
- 그리디
- 프로그래머스
- 큐
- SQL
- 다이나믹프로그래밍
- 자료구조
- 브루트포스알고리즘
- 논문리뷰
- 프로그래머스sql
- 백준
- 논문구현
- 해시를사용한집합과맵
- 백준알고리즘
- 이진탐색
- 정수론
- 프로그래머스연습문제
- 그리디알고리즘
- 문자열
- MySQL
- C언어
- 소수판정
- 수학
- 정렬
- Image Classification
- 사칙연산
- Today
- Total
초보 개발자의 이야기, 릿허브
[C++] 백준 11727번 2×n 타일링 2 본문
1. 문제이해

https://www.acmicpc.net/problem/11727
11727번: 2×n 타일링 2
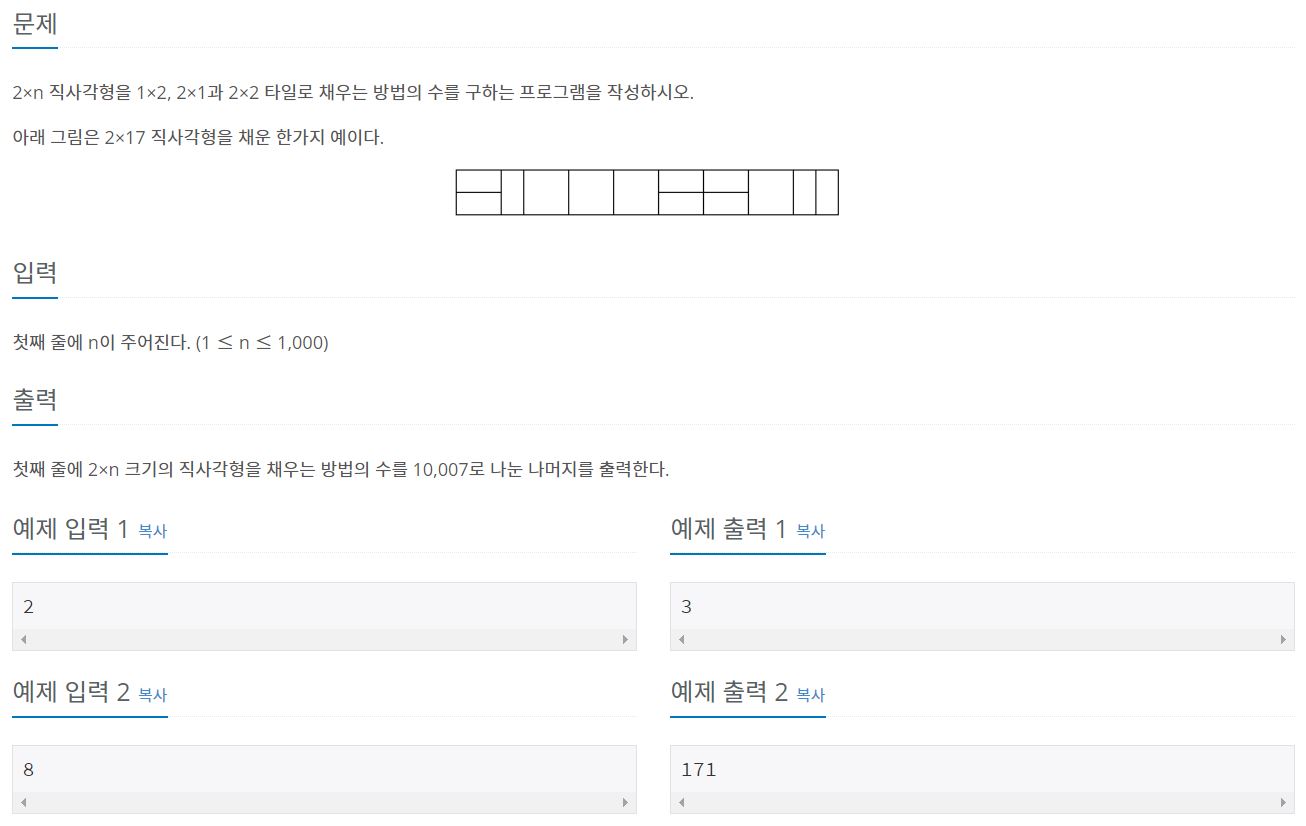
2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×17 직사각형을 채운 한가지 예이다.
www.acmicpc.net
주어진 n에 대해 2×n 크기의 직사각형을
1×2, 2×1, 2×2 타일로 채우는 방법의 수를 구하는 것이 목표이다.
단, 방법의 수를 10,007로 나눈 값을 출력해야 한다.
2. 문제풀이
이전에 풀이했던 11726번 문제와 거의 동일한 문제이다.
단, 하나의 조건이 추가되었는데, 바로 2×2 타일이다.
이전에는 1×2, 2×1 타일만을 가지고 타일링을 했다면, 이번에는 2×2 의 경우도 고려해주어야 한다.
풀이방법은 11726번과 상당히 동일하니, 문제에 대한 기본적인 이해는 아래 포스팅을 참고하자.
https://beginnerdeveloper-lit.tistory.com/91
[C++] 백준 11726번 2×n 타일링
1. 문제이해 11726번: 2×n 타일링 (acmicpc.net) 11726번: 2×n 타일링 2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운
beginnerdeveloper-lit.tistory.com

11726번 풀이에 사용했던 그림이다. 위 그림을 자세히 보면,
n번째 타일을 채우는 경우의 수 = (n - 1)번째 경우의 수 + (n - 2)번째 경우의 수 임을 알 수 있다.
이는, n - 1번째 경우들에 1×2 타일을 하나 추가한 것이 n번째 타일이 되고,
n - 2번째 경우들에 2×1 타일을 2개 추가한 것이 n번째 타일이 되기 때문이다.
여기에 위에서 언급한 2×2 타일의 경우가 추가된다고 하자.
2×2 타일의 경우, 가로, 세로의 길이가 2인 경우로, 2×1 타일이 2개 겹쳐진 경우와 동일하다.
1×2, 2×1 을 이용해 2×n 타일을 채우는 경우에 착안하여, 생각해보자.
1.
우선, (n - 1)번째 경우에 수에서 2×2 타일을 이용해 2×n타일을 만드는 것은 불가능하다.
(n-1)번째 경우의 수에서, 가로의 길이가 1만 부족한 경우이기 때문에,
해당 경우는 1×2 타일을 추가하는 경우만 그대로 남게 된다.
2.
(n-2)번째 경우의 수에서는 2×1 타일들 2개를 이용해 2×n 타일을 만들 수 있었다.
여기서, 2×2 타일은 2×1 타일이 2개 겹쳐진 경우와 동일하므로,
(n-2)번째 경우의 수에서 2×1 타일들 2개를 추가하는 경우, 2×2 타일을 추가하는 경우
같은 (n-2)번째 경우에 대해 2가지 경우가 발생하게 된다.
따라서, (n - 2)번째 경우의 수 X 2 만큼 발생하게 된다.
따라서, 2×n 크기의 타일을 1×2, 2×1, 2×2 타일로 채우는 방법의 수는 다음과 같다.
(n - 1)번째 경우의 수 + ((n - 2)번째 경우의 수 X 2)
3. 소스코드
#include <iostream>
using namespace std;
int main() {
int n;
int Rectangle[1000];
cin >> n;
Rectangle[0] = 0;
Rectangle[1] = 1;
Rectangle[2] = 3;
// n번째 타일을 채우는 경우의 수
// = (n - 1)번째 경우의 수 + ((n - 2)번째 경우의 수 X 2)
for (int i = 3; i <= n; i++) {
Rectangle[i] = (Rectangle[i - 1] + (Rectangle[i - 2] * 2)) % 10007;
}
cout << Rectangle[n];
return 0;
}배열 Rectangle을 선언하고, n을 입력받는다.
Rectangle[i]는 2×i 번째 직사각형을 1×2, 2×1, 2×2 타일로 채우는 방법의 수이다.
Rectangle[0], Rectangle[1], Rectangle[2] 값을 미리 선언해 준 뒤,
n번째 타일을 채우는 경우의 수 = (n - 1)번째 경우의 수 + ((n - 2)번째 경우의 수 X 2)를 적용해준다.
문제에서 해당 값을 10007로 나눈 나머지를 출력하라고 했으므로, %10007을 해주었다.
이전에 풀었던 2×n타일링 문제를 이해했다면 어렵지 않은 문제였다.
한 문제에 대한 연계문제들도 많이 있는것같으니, 많이 풀어봐야지💪
'코딩테스트 > 📗 백준 (BOJ)' 카테고리의 다른 글
| [C++] 백준 1316번 그룹 단어 체커 (0) | 2021.11.25 |
|---|---|
| [C++] 백준 4673번 셀프 넘버 (0) | 2021.11.24 |
| [C++] 백준1932번 정수 삼각형 (0) | 2021.11.16 |
| [C++] 백준 1149번 RGB거리 (0) | 2021.11.15 |
| [C++] 백준 1024번 수열의 합 (0) | 2021.11.12 |




