| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 정렬
- MySQL
- 이분탐색
- 프로그래머스코딩테스트
- SQL
- 논문구현
- 수학
- C
- 그리디
- Image Classification
- 백준알고리즘
- 소수판정
- 프로그래머스연습문제
- 브루트포스알고리즘
- C언어
- 해시를사용한집합과맵
- 자료구조
- 구현
- 프로그래머스sql
- 이진탐색
- 큐
- 정수론
- 백준
- 그리디알고리즘
- 문자열
- 사칙연산
- 다이나믹프로그래밍
- 프로그래머스
- C++
- 논문리뷰
- Today
- Total
초보 개발자의 이야기, 릿허브
[C++] 백준1932번 정수 삼각형 본문
1. 문제이해
https://www.acmicpc.net/problem/1932
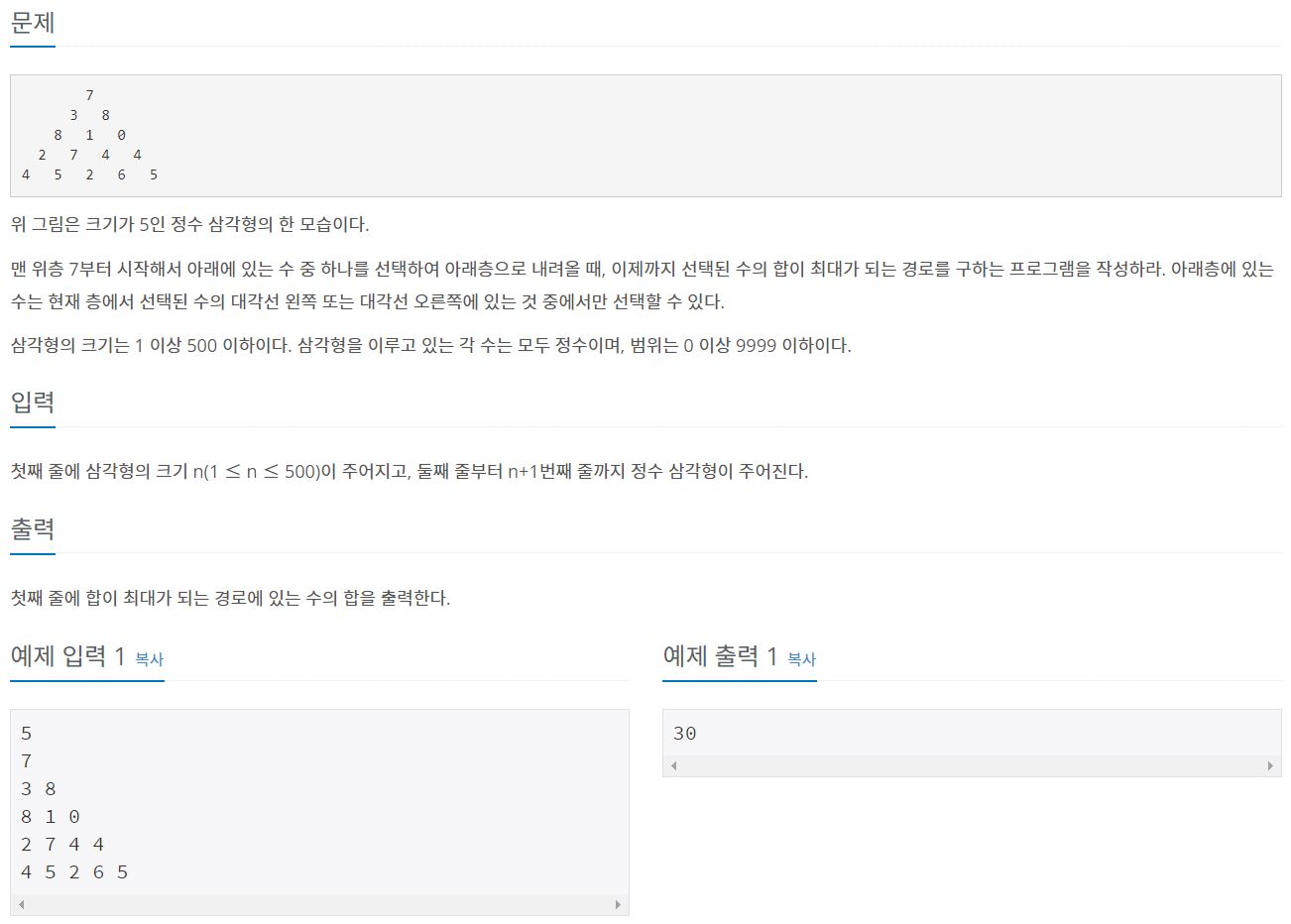
1932번: 정수 삼각형
첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.
www.acmicpc.net
정수 삼각형은 위 그림과 같이 i번째 줄에 i개의 정수로 이루어진 삼각형이다.
삼각형의 크기 n이 주어지고 맨 위층부터 시작해서
아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때,
이제까지 선택된 수의 합이 최대가 되는 경로에 있는 수의 합을 구하는 것이 목표이다.
단, 아래층에 있는 수는 현재 층에서 선택된 수의
대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다.
(삼각형의 크기(n)는 1 이상 500 이하이며,
삼각형을 이루고 있는 각 수는 모두 0 이상 9999 이하의 정수이다.)
2. 문제풀이
삼각형의 크기와 삼각형을 이루고 있는 정수들을 입력받아,
선택된 수의 합이 최대가 되는 경로에서의 수의 합을 출력하는 문제이다.
단, 경로는 맨 위층부터 시작해서, 대각선 왼, 오른쪽에 있는 숫자만 선택이 가능하다.
그렇다면, 어떻게 최댓값이 되는 경로를 찾을 수 있는지 아래 그림을 통해 자세히 살펴보자.

위와 같은 삼각형에서 맨 위의 값 ~ 맨 아랫값 중 하나에 도달하는 여러 경로 중 합이 최대인 경로를 찾아
해당 경로에서의 합을 구하는 것이 목표이다.
즉, 이 삼각형에서는 t[0][0] ~ t[3][j] 에 해당하는 경로 중 최대를 구하는 것이 목표이다.
t[3][j] 까지 향하는 각각의 경로들 중 최댓값은 다음과 같은 경우로 나누어 구할 수 있다.
1. 왼쪽 끝 값의 경우 (t[3][0]의 겅우)
: 삼각형의 맨 왼쪽 끝에 해당하는 경우로, 위 삼각형에서는 t[3][0]의 경우에 해당한다.
이 경우에는 오른쪽 위인 t[2][0]에서 오는 경로만 존재하므로, 해당 경우의 경로의 합의 최댓값은 다음과 같다.
(t[i][j] 까지의 최댓값) = (t[i - 1][j] 까지의 최댓값) + t[i][j]
2. 오른쪽 끝 값의 경우 (t[3][3]의 경우)
: 삼각형의 맨 오른쪽 끝에 해당하는 경우로, 위 삼각형에서는 t[3][3]의 경우에 해당한다.
이 경우에는 왼쪽 위인 t[2][2]에서 오는 경로만 존재하므로, 해당 경우의 경로의 합의 최댓값은 다음과 같다.
(t[i][j] 까지의 최댓값) = (t[i - 1][j - 1] 까지의 최댓값) + t[i][j]
3. 1, 2의 경우가 아닌 모든 경우 (t[3][1], t[3][2]의 경우)
: 1, 2에 해당하는 경우를 제외한 경우로, 삼각형의 맨 왼쪽도, 오른쪽에도 존재하지 않는 경우이다.
이 경우에는 해당 숫자의 왼쪽 위, 오른쪽 위에서 오는 경우 2가지가 존재하므로,
해당 경우의 경로의 합의 최댓값은 다음과 같다.
(t[i][j] 까지의 최댓값) = max(t[i - 1][j] 까지의 최댓값, t[i - 1][j - 1] 까지의 최댓값) + t[i][j]
위 3가지 경우를 이용해 t[3][j] 까지 향하는 각각의 경로들 중 최댓값을 구할 수 있다.
이렇듯, 마지막 줄에 있는 값까지의 최댓값 중 최대가 되는 값이,
최종적으로 구하고자 하는 합이 최대가 되는 경로의 최댓값이 된다.
위와 같이 정리한 3가지 경우를 참고하여 작성한 코드는 다음과 같다.
3. 소스코드
#include <iostream>
#include <algorithm>
using namespace std;
int triangle[500][500]; // 삼각형의 원소들
int tri_DP[500][500]; // 각 경우에서의 최대합
int main() {
int n; // 삼각형의 크기
int max_sum = 0; // 합이 최대가 되는 경로의 수의 합
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) {
cin >> triangle[i][j];
}
}
tri_DP[0][0] = triangle[0][0];
for (int i = 1; i < n; i++) {
for (int j = 0; j <= i; j++) {
// 1. 왼쪽 끝에 위치한 값일 경우
if (j == 0) {
tri_DP[i][j] = tri_DP[i - 1][j] + triangle[i][j];
}
// 2. 오른쪽 끝에 위치한 값일 경우
else if (j == i) {
tri_DP[i][j] = tri_DP[i - 1][j - 1] + triangle[i][j];
}
// 3. 위 두가지를 제외한 모든 경우
else {
tri_DP[i][j]
= max(tri_DP[i - 1][j - 1], tri_DP[i - 1][j])
+ triangle[i][j];
}
}
}
// tri_DP[n - 1][i]는 마지막 줄에 있는 각각의 값들까지의 최댓값
// 이들 중 최대가 되는 값이, 합이 최대가 되는 경로의 최댓값
max_sum = 0;
for (int i = 0; i < n; i++) {
if (tri_DP[n - 1][i] >= max_sum) {
max_sum = tri_DP[n - 1][i];
}
}
cout << max_sum;
return 0;
}먼저, 삼각형의 원소들에 해당하는 triangle[][]과,
각 원소까지의 최대 합에 해당하는 tri_DP[][]를 전역범위에서 선언했다.
(배열의 크기가 크기때문에, 스택 오버플로우 방지를 위해 전역범위에서 선언했다.)
메인 함수에서는 삼각형의 크기를 입력받고,
2. 문제풀이에서 구한 3가지 경우와 for문을 통해 각 원소까지의 최대 합(tri_DP)을 구해준다.
이후, 삼각형의 마지막 줄까지 연산이 끝나면,
tri_DP[n-1][i] 가 마지막 줄에 있는 각각의 값들까지의 최댓값이 되고,
이들 중 최댓값이 최종적으로 구하고자 하는 합이 최대가 되는 경로의 최댓값이 된다.
설명하기도 힘들었고,,, 합이 최대가 되는 경로의 최댓값,,,어쩌고,,,
열심히 쓴 글이 다 날아가서 다시 쓴 문제였다..😥
임시저장을 했는데도 날아가버려서 멘탈 와장창...
혹시나 이해가 안되는 부분이나 지적할 부분이 있다면 언제나 환영합니다.🥰
'코딩테스트 > 📗 백준 (BOJ)' 카테고리의 다른 글
| [C++] 백준 4673번 셀프 넘버 (0) | 2021.11.24 |
|---|---|
| [C++] 백준 11727번 2×n 타일링 2 (0) | 2021.11.22 |
| [C++] 백준 1149번 RGB거리 (0) | 2021.11.15 |
| [C++] 백준 1024번 수열의 합 (0) | 2021.11.12 |
| [C++] 백준 1181번 단어 정렬 (0) | 2021.11.09 |




