| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 논문구현
- 다이나믹프로그래밍
- Image Classification
- 프로그래머스
- 그리디
- 정수론
- 구현
- 프로그래머스연습문제
- C언어
- 해시를사용한집합과맵
- 프로그래머스sql
- MySQL
- 자료구조
- C++
- 이분탐색
- 정렬
- 문자열
- 백준
- 프로그래머스코딩테스트
- 브루트포스알고리즘
- 사칙연산
- 소수판정
- 이진탐색
- 큐
- 논문리뷰
- 백준알고리즘
- 수학
- SQL
- C
- 그리디알고리즘
- Today
- Total
초보 개발자의 이야기, 릿허브
[C++] 백준 1463번 1로 만들기 본문
1. 문제이해
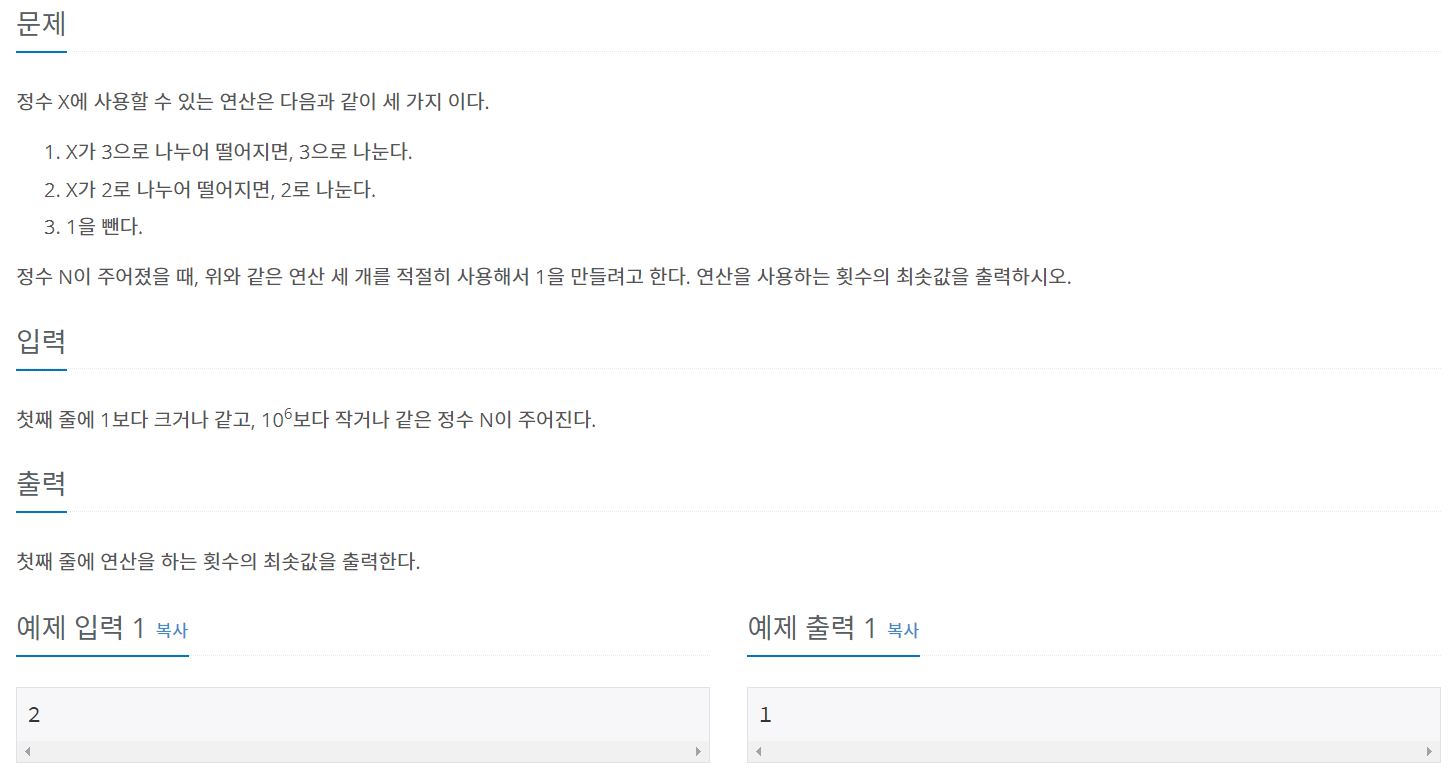
1463번: 1로 만들기
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
www.acmicpc.net
1. X가 3으로 나누어 떨어지면, 3으로 나눈다.
2. X가 2로 나누어 떨어지면, 2로 나눈다.
3. 1을 뺀다.
주어진 숫자 N을 위와 같은 연산을 이용해 1로 만드려고 할 때,
최소 몇 번의 연산이 필요한지를 출력하는 것이 목표이다.
2. 문제풀이
주어진 정수 N을 최소 몇 번의 연산 뒤에 1로 만들 수 있는지를 구하는 문제이다.
문제의 예제 입력 1의 경우인 2는,
"2. X가 2로 나누어떨어지면, 2로 나눈다" 에 의해 1번의 연산 후 1이 된다.
따라서, 최소 1번의 연산이 필요하게 된다.
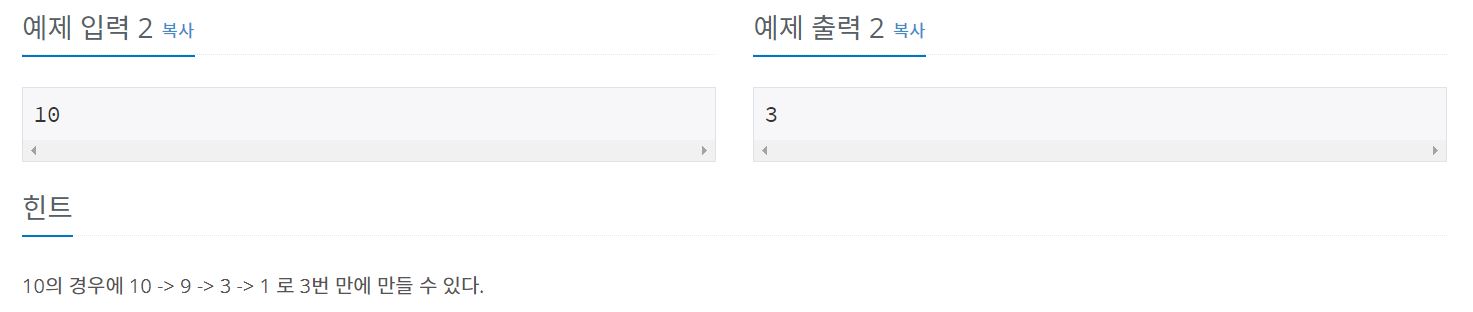
예제 입력 2의 경우인 10은,
"3. 1을 뺀다." (10 -> 9)
"1. X가 3으로 나누어 떨어지면, 3으로 나눈다." (9 -> 3)
"1. X가 3으로 나누어 떨어지면, 3으로 나눈다." (3 -> 1)
최소 3번의 연산이 필요하게 된다.
그렇다면, 과연 이러한 연산의 규칙은 어떻게 정하면 될까?
1, 2, 3은 모두 한번의 연산 후 1이 되는 관계로, 4부터 살펴보도록 하자.
< 4 >
4 -> 3 -> 1 OR 4 -> 2 -> 1
최소 2번의 연산 필요
(1을 빼면 3, 3으로 나누어지므로 3의 경우의 연산 + 1
2로 나누어지기도 하므로, 나눠진 2의 경우의 연산 + 1도 가능)
< 5 >
5 -> 4 -> 2 -> 1
최소 3번의 연산 필요
(5는 2, 3으로 나눌 수 없으므로 무조건 1을 빼고 시작해야 한다.
1을 빼면 4가 되므로, 이전의 4의 경우의 연산 + 1)
< 6 >
6 -> 2 -> 1 OR 6 -> 3 -> 1
최소 2번의 연산 필요
(3으로 나누어지므로, 3으로 나눈 2의 경우의 연산 + 1
2로 나누어지기도 하므로, 2로 나눈 3의 경우의 연산 + 1도 가능)
< 7 >
7 -> 6 -> 2 -> 1 OR 7 -> 6 -> 3 -> 1
최소 3번의 연산 필요
(7는 2, 3으로 나눌 수 없으므로 무조건 1을 빼고 시작해야 한다.
1을 빼면 6이 되므로, 이전의 6의 경우의 연산 + 1)
< 8 >
8 -> 4 -> 2 -> 1 OR 8 -> 4 -> 3 -> 1
최소 3번의 연산 필요
(8은 2로 나누어지므로, 2로 나눈 4의 경우의 연산 + 1)
위처럼, 4 ~ 8의 경우를 쭉 살펴보면 다음과 같은 규칙을 도출할 수 있게 된다.
N을 1로 만들기 위해 필요한 최소 횟수 = N - 1을 1로 만들기 위한 최소횟수 + 1
OR 2나 3으로 나누어지면, 나눠지고 남은 몫의 경우의 연산 + 1
두 경우중 더 작은 값을 선택해 취하면 되는 것이다. 이를 코드로 구현한 결과는 아래와 같다.
3. 소스코드
#include <iostream>
#include <algorithm>
using namespace std;
int DP[1000000];
int main() {
int N;
cin >> N;
for (int i = 2; i <= N; i++) {
// 1. 1을 뺀다.
DP[i] = DP[i - 1] + 1;
// 2. 2로 나누어지면
if (i % 2 == 0) {
DP[i] = min(DP[i], DP[i / 2] + 1);
}
// 3. 3으로 나누어지면
if (i % 3 == 0) {
DP[i] = min(DP[i], DP[i / 3] + 1);
}
}
cout << DP[N];
return 0;
}N을 입력받고, N을 1로 만들기 위한 최소 횟수의 배열을 DP라고 두었다.
2부터 시작해, 차례로 DP를 구해주고, 위 문제풀이에서 구한 규칙을 바탕으로,
N을 1로 만들기 위해 필요한 최소 횟수 = N - 1을 1로 만들기 위한 최소횟수 + 1
OR 2나 3으로 나누어지면, 나눠지고 남은 몫의 경우의 연산 + 1
를 적용해 코드로 구현했다.
이때, if문 안의 min을 통해 둘 중 더 적은 값을 채택하도록 해주었다.
DP문제는 언제 풀어도 역시나 어려운 것 같다..😭
점화식을 도출해내는 방법이 참 어려운 것 같고.. 문제도 어려운게 많은 것 같다.
앞으로 DP문제를 쭉 연습해 봐야할 듯 싶다..✍
'코딩테스트 > 📗 백준 (BOJ)' 카테고리의 다른 글
| [C++] 백준 9655번 돌 게임 (0) | 2021.10.11 |
|---|---|
| [C++] 백준 7795번 먹을 것인가 먹힐 것인가 (0) | 2021.10.08 |
| [C++] 백준 1620번 나는야 포켓몬 마스터 이다솜 (0) | 2021.10.05 |
| [C++] 백준 9461번 파도반 수열 (0) | 2021.10.01 |
| [C++] 백준 4948번 베르트랑 공준 (0) | 2021.09.30 |




